前面介紹的幾種濾波器都屬于平滑濾波器（低通濾波器），用來平滑圖像和抑制噪聲的；而銳化空間濾波器恰恰相反，主要用來增強圖像的突變信息，圖像的細節和邊緣信息。平滑濾波器主要是使用鄰域的均值（或者中值）來代替模板中心的像素，消弱和鄰域間的差別，以達到平滑圖像和抑制噪聲的目的；相反，銳化濾波器則使用鄰域的微分作為算子，增大鄰域間像素的差值，使圖像的突變部分變的更加明顯。

本位主要介紹了一下幾點內容：

?  圖像的一階微分和二階微分的性質

?  幾種常見的一階微分算子

?  二階微分算子 - Laplace 拉普拉斯算子

?  一階微分算子和二階微分算子得到邊緣的對比

一階微分和二階微分的性質

既然是基于一階微分和二階微分的銳化空間濾波器，那么首先就要了解下一階和二階微分的性質。

圖像的銳化也就是增強圖像的突變部分，那么我們也就對圖像的恒定區域中，突變的開始點與結束點（臺階和斜坡突變）及沿著灰度斜坡處的微分的性質。微分是對函數局部變化率的一種表示，那么對于一階微分有以下幾個性質：

?  在恒定的灰度區域，圖像的微分值為0.（灰度值沒有發生變換，自然微分為0）

?  在灰度臺階或斜坡起點處微分值不為0.（臺階是，灰度值的突變變化較大；斜坡則是灰度值變化較緩慢；灰度值發生了變化，微分值不為0）

?  沿著斜坡的微分值不為0.

二階微分，是一階微分的導數，和一階微分相對應，也有以下幾點性質:

?  在恒定區域二階微分值為0

?  在灰度臺階或斜坡的起點處微分值不為0

?  沿著斜坡的微分值為0.

從以上圖像灰度的一階和二階微分的性質可以看出，在灰度值變化的地方，一階微分和二階微分的值都不為0；在灰度恒定的地方，微分值都為0.也就是說，不論是使用一階微分還是二階微分都可以得到圖像灰度的變化值。

圖像可以看著是二維離散函數，對于圖像的一階微分其計算公式如下：
在x方向，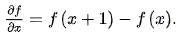
在y方向，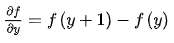

對于二階微分有:
在x方向，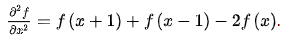
在y方向，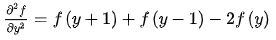

對于 圖像邊緣處的灰度值來說，通常有兩種突變形式：

?  邊緣兩邊圖像灰度差異較大，這就形成了灰度臺階。在臺階處，一階微分和二階微分的值都不為0.

?  邊緣兩邊圖像灰度變化不如臺階那么劇烈，會形成一個緩慢變換的灰度斜坡。在斜坡的起點和終點一階微分和二階微分的值都不為0，但是沿著斜坡一階微分的值不為0，而二階微分的值為0.

對于圖像的邊緣來說，通常會形成一個斜坡過度。一階微分在斜坡處的值不為0，那么用其得到的邊緣較粗；而二階微分在斜坡處的值為0，但在斜坡兩端值不為0，且值得符號不一樣，這樣二階微分得到的是一個由0分開的一個像素寬的雙邊緣。也就說，二階微分在增強圖像細節方面比一階微分好得多，并且在計算上也要比一階微分方便。

梯度圖

在圖像處理中的一階微分通常使用梯度的幅值來實現。對于圖像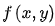,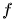在坐標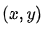處的梯度是一個列向量

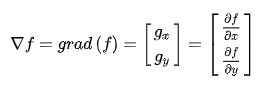
該向量表示圖像中的像素在點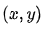處灰度值的最大變化率的方向。
向量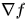的幅值就是圖像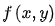的梯度圖，記為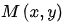

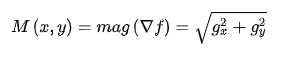
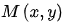是和原圖像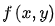同大小的圖像。由于求平方的根運算比較費時，通常可以使用絕對值的和來近似

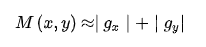
從上面可以看出，要得到圖像的梯度圖，有以下步驟：

?  圖像在x方向的梯度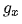

?  圖像在y方向的梯度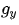

?  

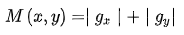
一階梯度算子

圖像是以離散的形式存儲，通常使用差分來計算圖像的微分，常見的計算梯度的模板有以下幾種

?  根據梯度的定義

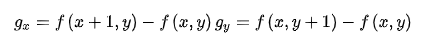
可以得到模板 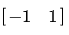和 。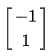
使用該方法計算的圖像的梯度只是考慮單個像素的差值，并沒有利用到圖像的像素的鄰域特性。

?  Robert交叉算子
在圖像處理的過程中，不會只單獨的對圖像中的某一個像素進行運算，通常會考慮到每個像素的某個鄰域的灰度變化。因此，通常不會簡單的利用梯度的定義進行梯度的計算，而是在像素的某個鄰域內設置梯度算子。考慮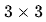，區域的像素，使用如下矩陣表示：

令中心點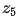表示圖像中任一像素，那么根據梯度的定義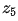，在在x和y方向的梯度分別為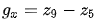：和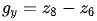，梯度圖像M(x,y)

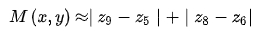
根據上述公式，Robert在1965年提出的Robert交叉算子

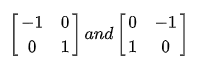
?  Sobel算子
Robert交叉算子的尺寸是偶數，偶數尺寸濾波器沒有對稱中心計算效率較低，所以通常濾波器的模板尺寸是奇數。仍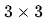以為例，以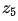為對稱中心（表示圖像中的任一像素），有

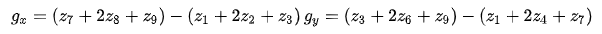
利用上述公式可以得到如下兩個卷積模板，分別計算圖像在x和y風向的梯度

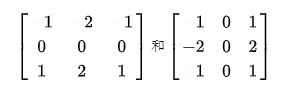
第一個模板，第三行和第一行的差近似x方向的偏微分；第二個模板，第三列和第一列的差近似y方向的偏微分，而且模板的所有系數只和為0，表示恒定灰度區域的響應為0.

基于OpenCV的一階梯度算子實現

?  Sobel算子
在OpenCV中封裝了Sobel算子，其函數為Sobel。使用Sobel能夠很方便的計算任意尺寸的x和y方向的偏微分，具體如下：

void sobel_grad(const Mat &src, Mat &dst)
{
    Mat grad_x, grad_y;

    Sobel(src, grad_x, CV_32F, 1, 0);
    Sobel(src, grad_y, CV_32F, 0, 1);
    
    //convertScaleAbs(grad_x, grad_x);
    //convertScaleAbs(grad_y, grad_y);
    //addWeighted(grad_x, 0.5, grad_y, 0.5, 0, dst);

    magnitude(grad_x, grad_y, dst);
    convertScaleAbs(dst, dst);
}

上述代碼中調用Sobel分別得到圖像在x和y方向的偏微分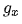和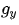，然后相加得到得到圖像的梯度圖。
其余的幾個函數說明,convertScaleAbs將圖像類型轉換為CV_8U；addWeighted按一定的權值將兩個圖像相加；magnitude求兩個圖像的幅值，其公式為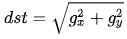，具體的參數說明可參考OpenCV的官方文檔。

?  基于定義和Robert交叉算子的計算
對于這兩種算子，OpenCV中并沒有提供具體的函數，不過可以利用filter2D函數來實現。filter2D是OpenCV中對圖像進行卷積運算的一個很重要的函數，該函數能夠使用任意的線性卷積核對圖像進行卷積運算。

void robert_grad(const Mat& src, Mat &dst)
{
    Mat grad_x, grad_y;

    Mat kernel_x = (Mat_<float>(2, 2) << -1, 0,0,1);
    Mat kernel_y = (Mat_<float>(2, 2) << 0, -1, 1, 0);
    
    filter2D(src, grad_x, CV_32F, kernel_x);
    filter2D(src, grad_y, CV_32F, kernel_y);

    //convertScaleAbs(grad_x, grad_x);
    //convertScaleAbs(grad_y, grad_y);
    //addWeighted(grad_x, 1, grad_y, 1, 0, dst);
    magnitude(grad_x, grad_y, dst);
    convertScaleAbs(dst, dst);
}

構造好Robert交叉算子，然后調用filter2D即可；基于定義的計算方法于此類似，不在贅述。

結果三種方法計算得到的梯度圖，如下：

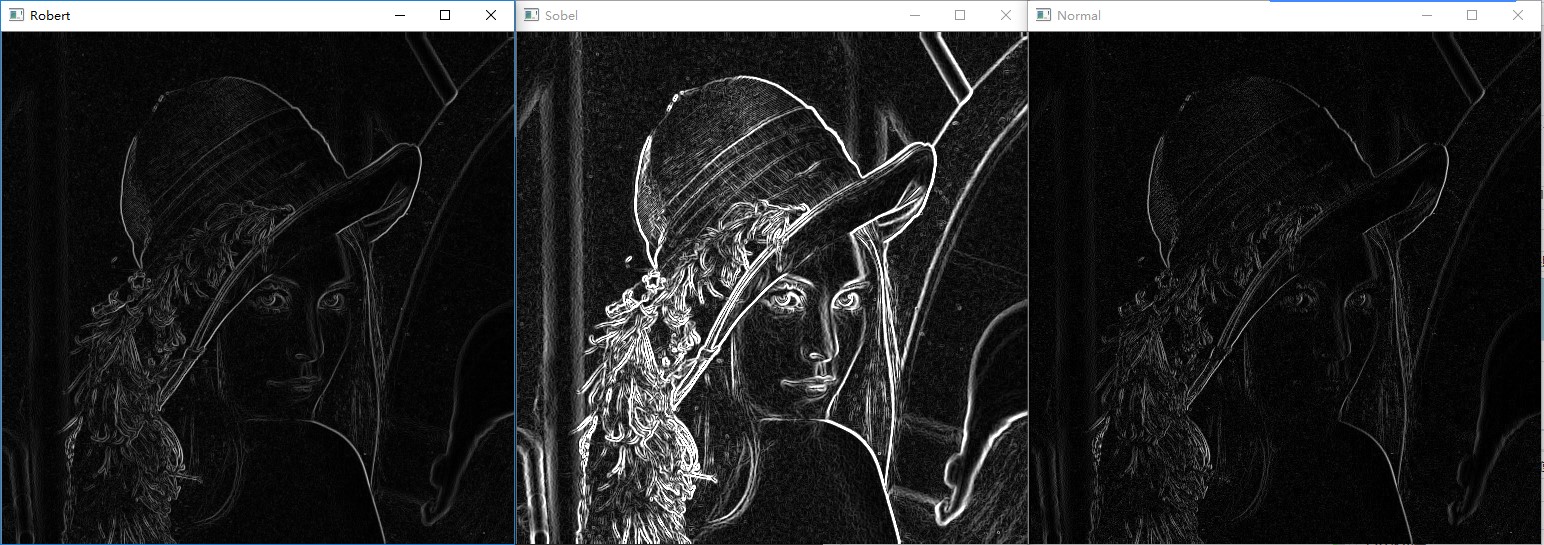
從上面結果可以看出，Robert交叉算子和基于定義得到的邊緣圖，得到的邊緣較細并且不是很連續；Sobel得到邊緣較粗，線條連續，效果明顯好于其他的兩種算子。

二階微分算子 - LapLace 拉普拉斯算子

二階微分算子的代表就是拉普拉斯算子，其定義如下：

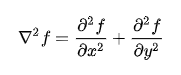
其中：

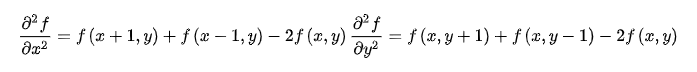
對于上述的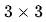區域，則有

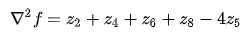
其得到的模板如下：

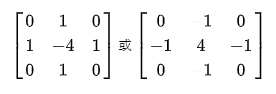
注意，模板中心的符號，并且模板的所有系數之和為0.

在OpenCV中有對LapLace的封裝，其函數為Laplacian,其使用的模板中心的系數為負，具體參數說明參見OpenCV文檔，其得到的邊緣圖和一階微分算子得到邊緣圖對比結果如下：

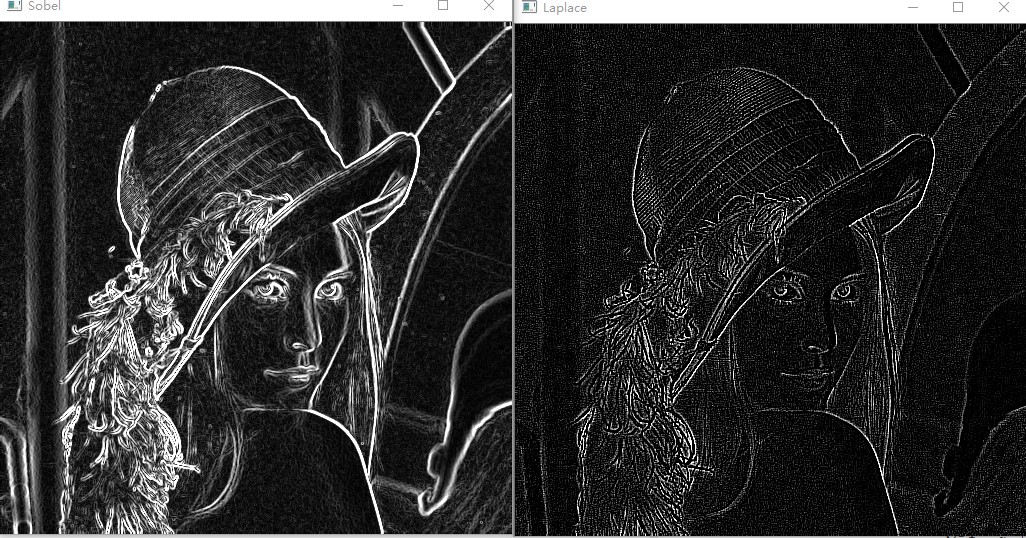
?  一階微分算子Sobel得到的邊緣較粗

?  二階微分算子Laplace得到的邊緣則較細，并且邊緣是雙邊緣

?  Lpalace算子對噪聲比較敏感，得到的邊緣圖像上噪聲較明顯

由于Laplace算子對噪聲敏感，會得到雙邊，并且并不能檢測邊緣的方向，其通常不用于直接的邊緣檢測，只是起到輔助作用。檢測某像素實在邊緣的亮的一側還是暗的一側，利用“零跨越”確定邊緣的位置。

總結

本文主要介紹了圖像空間域的銳化算子（也就是邊緣檢測算子），這些算子都是基于圖像的微分的：一階微分和二階微分（拉普拉斯算子）。
由于一階微分和二階微分有各自的特點，其得到的圖像邊緣也不相同：一階微分得到的圖像邊緣較粗，二階微分得到的是較細的雙邊緣，所以在圖像的邊緣增強方面二階微分算子的效果較好。

文章轉自Brook_icv   https://www.cnblogs.com/wangguchangqing/p/6947727.html

void sobel_grad(const Mat &src, Mat &dst)
{
    Mat grad_x, grad_y;

    Sobel(src, grad_x, CV_32F, 1, 0);
    Sobel(src, grad_y, CV_32F, 0, 1);
    
    //convertScaleAbs(grad_x, grad_x);
    //convertScaleAbs(grad_y, grad_y);
    //addWeighted(grad_x, 0.5, grad_y, 0.5, 0, dst);

    magnitude(grad_x, grad_y, dst);
    convertScaleAbs(dst, dst);
}

void robert_grad(const Mat& src, Mat &dst)
{
    Mat grad_x, grad_y;

    Mat kernel_x = (Mat_<float>(2, 2) << -1, 0,0,1);
    Mat kernel_y = (Mat_<float>(2, 2) << 0, -1, 1, 0);
    
    filter2D(src, grad_x, CV_32F, kernel_x);
    filter2D(src, grad_y, CV_32F, kernel_y);

    //convertScaleAbs(grad_x, grad_x);
    //convertScaleAbs(grad_y, grad_y);
    //addWeighted(grad_x, 1, grad_y, 1, 0, dst);
    magnitude(grad_x, grad_y, dst);
    convertScaleAbs(dst, dst);
}

void robert_grad(const Mat& src, Mat &dst)
{
    Mat grad_x, grad_y;

    Mat kernel_x = (Mat_<float>(2, 2) << -1, 0,0,1);
    Mat kernel_y = (Mat_<float>(2, 2) << 0, -1, 1, 0);
    
    filter2D(src, grad_x, CV_32F, kernel_x);
    filter2D(src, grad_y, CV_32F, kernel_y);

    //convertScaleAbs(grad_x, grad_x);
    //convertScaleAbs(grad_y, grad_y);
    //addWeighted(grad_x, 1, grad_y, 1, 0, dst);
    magnitude(grad_x, grad_y, dst);
    convertScaleAbs(dst, dst);
}